（形の科学会の会報「形の科学会誌」 第13号 第3号 （1998）に、小川先生がこの問題についてのコメントを発表されました。先生のお許しを得て、「最近気付いたこと」に全文を引用させていただきました。このコメントによれば、専門家的な発想では、この問題は実験式という便法に頼るべき種類のものであり、証明するような種類の問題ではないとのことでした。）
以下に私の式の証明を示します。
考え方は、対称面の辺の数が、一つの正多面体については、一定であることを利用したものです。
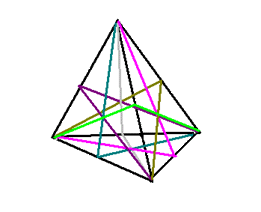まず、最も簡単な例である右の正4面体の図を見てください。色の付いた線は、対称面の切片です。この図をじっと見ると分かるのですが、対称面はすべて3角形（上の表では、対称面の辺の数が3となっています）で、その1辺は、立体の稜（二つの頂点を結ぶ線）に一致して、残りの辺はともに、表面を構成する正三角形の対称線と一致しています。また、すべての対称線と稜は、どれか一つの対称面に対応しており、一つの稜または対称線を二つの対称面が通ることはありません。これから、正4面体の場合には、
対称面の数（6）×対称面の辺の数（3）
＝稜の数（6）＋｛表面を構成する面の数（4）×この面の対称線の数（3）｝
という関係が成立することがわかります（正4面体の場合この式の値は18となります）。
ここで指摘したような関係に似た関係は、すべての正多面体にも当てはまりますので、この式もすべての正多面体に当てはまることになります（場合によっては、同じ正多面体の対称面の切片が、すべて稜であったり、一部だけ稜であったり、すべて対称線であることもありますが、辺の数は同じになっています）。
次に、両辺を対称面の辺の数で割ると、対称面の数を求める式ができます。
対称面の数＝〔稜の数＋｛表面を構成する面の数×この面の対称線の数｝〕 /対称面の辺の数
この式で稜の数（a）と表面を構成する面の対称線の数（b）は、正n面体で表面を構成する面が正p角形である場合にはすぐに分かります。
稜の数（a）・・・・すべての正多面体のすべての稜は二つの正多角形の辺となっています。そのため、面の数にその面の辺の数を掛けて2で割れば、稜の数が求まることになります。
a＝n×p/2
正多角形の対称線の数（b）・・・・正p角形の対称線の数は、p本となっています。
そこで、対称面の数の式にこれらを代入しますと、
対称面の数＝｛n×p/2＋（n×p）｝/q＝3np/2q
となり私の式が得られます。
先生からいただいたメールによりますと、この問題は、11月20、21日に東京の統計数理研究所で開催された、形の科学シンポジウムの際に配布された「形の科学会誌」86ページに紹介されたそうです。どうもご協力ありがとうございました。恐ろしく簡単になった、先生の式の証明も、お送りいただき次第、掲載させていただきたいと考えております（98年12月4日）。
小川先生の式と、私が思い付いたと思っていた式の証明が載っている本を守川穣様がお教えくださいました・・・詳しくは「最近気付いたこと」の 問題24（数学）の解答が載っている本を守川穣様がお教えくださいました をご参照ください（2002年10月28日追記）。
