問題24(数学)の解答が載っている本を守川穣様がお教えくださいました 問題24(特別クイズ、数学) には、「形の科学会」会長の筑波大学物理工学系教授 小川 泰先生が正解をお寄せくださったことは、問題文や、「最近気付いたこと」の「問題24についての小川教授のコメント」 にもご紹介させていただきました。問題は、正多面体の対称面の数を計算する式を考えていただくというものでした。ただ、小川先生のお答えは、私が考えていた答えとは異なり、私のものよりも非常に簡単な式でした。また、その式が正しく対称面の数を与えることは分かるのですが、なぜその式によって正解が与えられるのかが分からないまま4年が過ぎてしまいました。
問題24は,4年近く前の問題ですが,「小川先生のコメントに対する印象」の個所に書いてある事項は,その後,進展しましたか.
対称面に含まれている稜の数
対称面に直交している稜の数
切り口が長方形の対称面
2個
0個
切り口が正方形の対称面
0個
4個
他の正多面体の場合も,同様な記法が用いられています.
守川穣様は、現在でも、正多面体に関連した(正確には、正多面体の4次元版である正多胞体(の3次元空間への投影)についての)研究を続けられており、その成果をご自身のホームページ( http://www.h4.dion.ne.jp/~morikawa/ ) に公開されています。グラフィックス・ソフトについてのご著書(『2&3次元グラフィックス・ソフトの基礎と応用 パソコンによるコア・システムの実現とその活用法』CQ出版社刊、『PC-9801 3次元グラフィックス入門』アスキー出版局刊など)もあります。
小川先生の式の証明
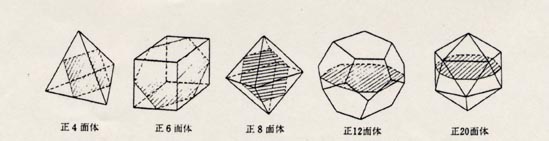
以下の証明では、いろいろな変数について、私が勝手に決めた記号を使うのはやめて、標準的な記号を使うことにしました。小川先生もおっしゃっているように、正p角形q個が各頂点に集まって、正多角錐(ただし、普通の多角錐のように底は平らとは限りません)を形成している正多面体は、(p,q)と表されます。この表記を使うと、正4面体は(3,3)、正6面体は(4,3)、正8面体は(3,4)、正12面体は(5,3)、正20面体は(3,5)と表されます。V 、辺(edge)の数はE 、面(face)の数はF m 、対称面の辺数(辺の数)はL (正式には小文字が使われているようですが、見にくくなるため大文字にしました)、ペトリー多角形 の辺数を h ,その個数を n という記号を使うことにします。ペトリー多角形 回映面 と呼ばれるそうです)。
正多面体 p q V E F m L h n
正4面体
3
3
4
6
4
6
3
4
3
正6面体
4
3
8
12
6
9
4
6
4
正8面体
3
4
6
12
8
9
4
6
4
正12面体
5
3
20
30
12
15
6
10
6
正20面体
3
5
12
30
20
15
6
10
6
この表から対称面の数mについて、
ペトリー多角形の辺数 h と 正多面体の辺数 E の関係
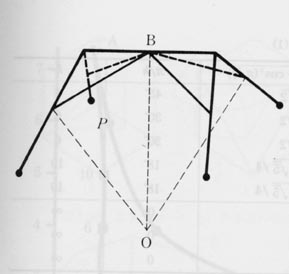
正多面体の各辺の中点の一つを B 点とし、正多面体の中心を O 点とします。B
点を通るペトリー面は、2枚しかないことが左の図から分かります(この図は、「正多面体を解く」の45ページからコピーさせていただきました)。また、O
点について B 点と対称な位置に、別の辺の中点があります。 一つのペトリー多角形の相対する一対の頂点(h/2組)に、他のn-1枚のペトリー多角形の頂点が交わるので
n-1=h/2となります。
(2) の n に (1) を代入すると。対称面の数 m とペトリー多角形の辺数 h の間の関係
各面がp角形、各頂点がq角錐の多面体では各面に辺がp本ずつあり、各辺は2面ずつに共通ですから、次式が成り立ちます。
(5) のpF に (6)を代入すると、ここでは、説明用に上で示した正6面体(立方体)の図を用いましたが、導いてある関係式は、すべての正多面体について成り立ちます。
守川先生、ご親切にこの問題の答えが載っている本を教えていただいただけでなく、コピーを取って、分かりやすい添え書きまでしていただいたものを送っていただいて本当にありがとうございました。先生には、お礼を差し上げたいと申し上げたのですが、固辞されましたので、残念ながら、心からお礼を申し上げるだけとさせていただきます。
守川先生からメールをいただきました(2002年11月4日追記) 青字 になっています)。また、オイラーの公式についてのコメントもいただきましたので、以下でご紹介させていただきます。
ここでのオイラーの公式は、一般にはオイラーの多面体公式と呼ばれています。ポアンカレーはこの公式を、一般の次元の場合に拡張していて、拡張された公式はオイラー-ポアンカレーの公式と呼ばれています。点、辺、面、...の数を、N0,N1,N2,...として、
以上が先生のコメントです。問題45(教育) およびその解答の最後の部分 をご参照ください)などという話を外国人にすると、一様に信じられないという言葉が返ってきます。
コンピュータ・グラフィクスによる各正多面体の対称面とペトリー多角形の画像を守川先生をお送りくださいましたので、「最近気付いたこと」の正多面体のコンピュータ・グラフィクス画像 に掲載しました(2003年5月10日追記)。
・最初のページに戻る
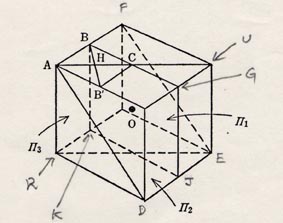 ペトリー多角形の各頂点、つまり正多面体の辺の中点(この場合Bを考えます)を通る対称面は2枚ずつあります(AFEDとBGJK)。ACとBB'の交点Hを通る対称面は、ACを含む1枚(AUER)のみです。ただし、ペトリー多角形の相対する一対の点は同じ対称面に対応しますので、対称面の数
m は
ペトリー多角形の各頂点、つまり正多面体の辺の中点(この場合Bを考えます)を通る対称面は2枚ずつあります(AFEDとBGJK)。ACとBB'の交点Hを通る対称面は、ACを含む1枚(AUER)のみです。ただし、ペトリー多角形の相対する一対の点は同じ対称面に対応しますので、対称面の数
m は